A few days ago, I found myself thinking about free monads, specifically Prompt monads, and wondering if there were equivalents for applicative functors. I didn’t realize it at the time, but apparently there was a recent bit of discussion about this in the Haskell community, starting with a blog post by Tom Ellis, and leading to a roundup of implementations by Roman Cheplyaka.
The consensus implementation, at least the one provided by the free package, looks roughly like this:
> {-# LANGUAGE GADTs, RankNTypes #-}
>
> module FreeApp where
>
> import Control.Applicative
>
> data Free f a where
> Pure :: a -> Free f a
> App :: f a -> Free f (a -> b) -> Free f b
>
> liftFree :: f a -> Free f a
> liftFree x = App x (Pure id)
>
> lowerFree :: Applicative f => Free f a -> f a
> lowerFree (Pure x) = pure x
> lowerFree (App x xs) = x <**> lowerFree xs
>
> instance Functor (Free f) where
> fmap f (Pure a) = Pure (f a)
> fmap f (App x xs) = App x (fmap (f .) xs)
>
> instance Applicative (Free f) where
> pure = Pure
>
> Pure f <*> y = fmap f y
> App x xs <*> y = App x (fmap flip xs <*> y)Essentially, Free f a consists of a sequence of “effects” (values of type f a, for some a) and a function which combines the results of those effects to produce the final answer.
You can also see that this is going to have bad asymptotic performance. fmap f x, for example, will take time O(n) time, where n is the number of effects in x. Worse, x <*> y will take O(n2 + m) time, since it calls fmap n times on x and once on y.
My first implementation
Of course, I didn’t bother to look for other implementations until after I’d found my own. I think I considered one like Free above, but rejected it because I didn’t like that fmap was so expensive. Instead, I kept the function separate from the effect sequence. To make it easy to call fmap without needing to walk the tree, I made the function accept all the results from the effects in a single argument, represented as a nested tuple.
Here’s the type for the effect sequence:
> data CSeq f a where
> CNil :: CSeq f ()
> CCons :: f a -> CSeq f u -> CSeq f (a,u)
>
>
> reduce :: Applicative f => CSeq f u -> f u
> reduce CNil = pure ()
> reduce (CCons x xs) = (,) <$> x <*> reduce xsSo if we have operations x :: f a, y :: f b, and z :: f c, we can put them in sequence and get CCons x (CCons y (CCons z CNil)) :: Seq f (a,(b,(c,()))).
And here’s the implementation itself:
> data C1 f a = forall u. C1 (u -> a) (CSeq f u)
>
> liftC1 :: f a -> C1 f a
> liftC1 a = C1 fst (CCons a CNil)
>
> lowerC1 :: Applicative f => C1 f a -> f a
> lowerC1 (C1 f x) = f <$> reduce x
>
> instance Functor (C1 f) where
> fmap f (C1 u x) = C1 (f . u) x
>
> instance Applicative (C1 f) where
> pure a = C1 (const a) CNil
>
> C1 f x <*> C1 g y = rebaseC1 x C1 (\v u -> f u (g v)) y
>
> rebaseC1 :: CSeq f u -> (forall x. (x -> y) -> CSeq f x -> z) ->
> (v -> u -> y) -> CSeq f v -> z
> rebaseC1 CNil k f = k (\v -> f v ())
> rebaseC1 (CCons x xs) k f =
> rebaseC1 xs (\g s -> k (\(a,u) -> g u a) (CCons x s))
> (\v u a -> f v (a,u))(The prefix C, incidentally, stands for “Curry”, because when I was naming it, I got currying and uncurrying confused. C1 uses an uncurried function; Free uses a curried one.)
The only real tricky part is rebaseC1. It may not be obvious, but it essentially acts like ++, traversing the first sequence and creating a new one by appending the second sequence. The difference is that this also has to modify the return functions and that the return type depends on the input types. I could have used type families here, but for some reason I chose to just stick with existential types; the continuation passed in the second argument is polymorphic in the sequence type, allowing me to just pass C1 when I call it.
The real “trick” in rebaseC1 involves the y parameter, which changes in the recursive call to allow us to pass values through the later parts of the computation and then reconstruct them. So if the third parameter, f has type v -> (a,u) -> y, in the recursive call it will have type v -> u -> a -> y. The modified continuation will eventually convert the function g :: x -> a -> y into a one with type (a,x) -> y and pass it to the original continuation.
Asymptotically, this is more efficient than Free. All of the operations are O(1), aside from lowerC1 and <*>, which are O(n). It’s pretty clear that O(n) is the best something like lowerC1 could be, since it has to evaluate every effect, but can we get a faster <*>?
My second implementation
Consider that <*> is essentially appending one sequence to another. In lists, appending works by replacing the final [] of the first list with the second list. That is,
1:2:3:[] ++ 4:5:[] = 1:2:3:4:5:[]We can speed up append by taking the end of the list as a parameter, allowing us to use [] or another list as we choose. Then appending simply becomes function composition.
(\n -> 1:2:3:n) . (\n -> 4:5:n) = (\n -> 1:2:3:4:5:n)Finding an analogous trick for C1 is harder, obviously, but after a bunch of tweaking, this is what I came up with:
> newtype C2 f a = C2
> { unC2 :: forall u y z.
> (forall x. (x -> y) -> CSeq f x -> z) ->
> (u -> a -> y) -> CSeq f u -> z }
>
> liftC2 :: f a -> C2 f a
> liftC2 a = C2 (\k f s -> k (\(a,s) -> f s a) (CCons a s))
>
> lowerC2 :: Applicative f => C2 f a -> f a
> lowerC2 x = unC2 x (\f s -> f <$> reduce s) (\() -> id) CNil
>
> instance Functor (C2 f) where
> fmap g x = C2 (\k f -> unC2 x k (\s -> f s . g))
>
> instance Applicative (C2 f) where
> pure a = C2 (\k f -> k (flip f a))
>
> x <*> y = C2 (\k f -> unC2 y (unC2 x k) (\s a g -> f s (g a)))Now, all operations are O(1) except lowerC2.
As a quick explanation, x :: C2 f a is a function taking three arguments. The first is a continuation (of the same type used in reduceC1) saying what to do with the final effect sequence and function. The third is the tail of the effect sequence, that x can add to using CCons. The second is a function which explains how to take the results of the tail effects and the value produced by x and combine them into the final return value. You can look at liftC2 and pure to see how they use them.
<*> uses the same trick as rebaseC1 of being sneaky with the y type parameter, allowing us to pass an extra value from x to y. That’s also why the function doesn’t have the seemingly more logical argument order a -> u -> v.
Notice in <*> that the first argument is put into the continuation of the second one. This is the secret to C2’s speed: it essentially traverses the expression tree from right to left, building the sequence of events from last to first. Unlike Free or C1, C2 never has to traverse and reconstruct the effect sequence.
Naturally, C1 and C2 are easily interconvertible:
> c2toC1 :: C2 f a -> C1 f a
> c2toC1 x = unC2 x C1 (\() a -> a) CNil
>
> c1toC2 :: C1 f a -> C2 f a
> c1toC2 (C1 g x) = C2 (\k f -> rebaseC1 x k (\v u -> f v (g u)))Testing for speed
I’ve talked a bit about asymptotic performance, but that isn’t the end of the story with efficiency. C1 and C2 do a bit work converting functions between curried and uncurried forms, so we should do some experiments to see whether they’re actually any better.
Here’s one. I generated a balanced binary tree containing between 10 and 100 nodes, each of which is a trivial call to liftX, used sequenceA to traverse the tree, and then used lowerX to run the computation. I then used Criterion to tell me how long they took. The result was that C2 was easily faster than C1, which was much faster than Free.
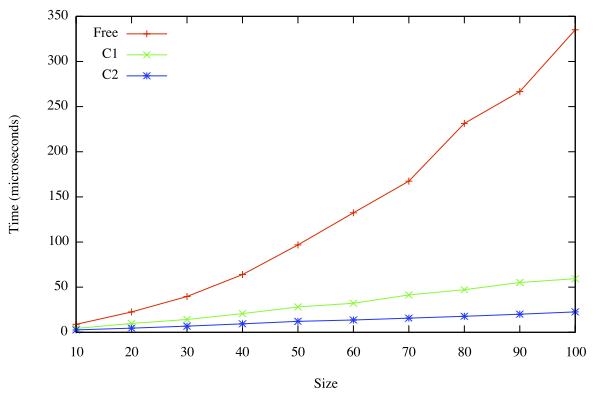
Other experiments are more stark. For example, expressions of the form
f <$> lift () <*> lift () <*> lift () …are something of a worst case for Free and C1, particularly as the number of arguments rose. In my experiments, the time for Free went from 0.58 μs to 14 μs as the number of arguments rose from 3 to 11. C2, in contrast, rose only from 0.049 μs to 0.16 μs.
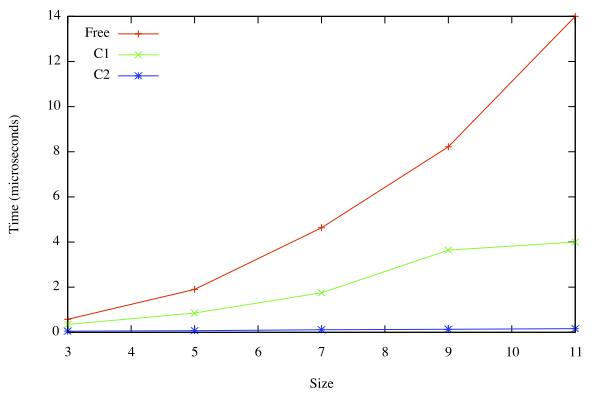
Obviously, this experiment is artificial, but its results hold up in the tree traversal experiment.
The funny thing is, if I had started my exploration by looking for other implementations, I might have found the existing ones and stopped, my curiosity satisfied. Because I was (re)inventing the concept for myself, I pushed harder to find the best one I could.1 The results are a significant improvement over the current state of the art.
It may be that no one will ever need a free applicative functor. It certainly may be that no one will need the speed improvement of C2 over Free. We’ve still learned two lessons here: don’t append when you can compose, and don’t use curried functions if you’re going to compose them.
I'm omitting, in fact, four implementations I came up with that use a curried function—in fact,
C1andC2were renamed to contrast with them. When I finally pulled out Criterion, I saw that they could beatFree, butC2was better than all of them. Since they’re also more complicated, it didn’t seem worth it to mention them.↩