Loop the Lab

A Mechanics Lab Using Hot Wheels® Cars

Dave Van Domelen, The Ohio State University

Adapted from talk GD6 at the AAPT National Meeting in Denver, August 16, 1997
Supported by NSF Grants DUE9396205 and GER9553460

Background

As part of the Gateway Project at The Ohio State University, I designed a course of mechanics labs to helps students strengthen their abilities in the following areas:

After investigating several options, I settled on a course mainly using Hot Wheels® toys, rulers and timers. No computers or sophisticated measuring equipment. The idea behind this was twofold: help students become comfortable using less than optimal data, and give them opportunities to find ways around deficiencies in their measuring devices.

The students did not have a lab manual for this course, rather they were given a task or tasks to perform using the available equipment, and were responsible for designing their own experiments. Over the course of the term they were slowly introduced to the various elements of the lab, often finding that seemingly trivial tasks required a great deal of thought on their parts. By the eighth week of the quarter, they were comfortable enough with the format of the lab that they had little trouble with the loop lab described below.

Before presenting the lab, it's worth noting that the TA was very active in the course of this class, shuttling from group to group to engage them in Socratic dialogue and draw out concepts the students were struggling with. The lack of a lab manual simply recognizes that there are so many different questions the students might have that a book trying to cover them would be unwieldy, especially if written in such a way as to actively engage the students. Instead, the TAs cover questions as they arise.

The Lab: Energy in a Vertical Loop

Equipment

Per group:

Tasks

Procedure

Part A

Students were rather resourceful in designing experiments to determine the energy levels of the launcher, with designs falling into four main categories:
  1. Launch straight up. Change in height was used to find change in gravitational potential energy, which was then set equal to the spring potential energy of that setting. Several groups first got a rough estimate by watching the car fly up past a ruler, then ran a second trial while holding a piece of paper or cardboard at the previously observed level. If the car hit the cardboard, it was raised slightly and another launch made.
  2. Launch up steep incline. A piece of track was taped to a long ruler and placed at a steep angle. Students had to account for friction turning some of the initial energy to heat, but this method was less "messy" than the first.
  3. Ballistic I. The launcher was placed at the edge of the table at a 45 degree angle, and the landing point of the car measured. Using ballistics equations, the group determined the launch velocity and hence the initial kinetic energy. This kinetic energy was set equal to the initial spring potential energy of the launcher setting.
  4. Ballistic II. Cars were simply shot off the edge of the lab table. Given their initial height, the time to fall to the floor could be calculated. This time was then combined with the horizontal distance traveled to determine initial speed, and hence kinetic energy.
Once the design was approved, the students performed their experiments and determined the energies. Typical results were on the order of .01 Joules.

Part B

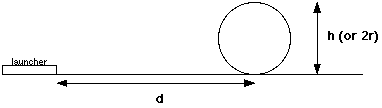Experimental Diagram, click on to download
Students were told to construct the track shown above, using about a meter of track between the launcher and the loop. Some groups compensated for the height of the connection from the launcher to the track by placing the track (and loop) on a bed of notebooks or cardboard sheets so there would be no extra change in height.

The first thing that students had to realize for this task was that in order for the car not to lose contact with the track, the normal force had to be zero or greater, which led to a calculation of the minimum speed required at the top of the track. This minimum speed could also be converted to a minimum kinetic energy.

Next, the students needed to determine how much initial kinetic energy would be converted to other forms, such as gravitational potential and heat. Energy due to gravitational potential was simply mgh, and students knew how to account for frictional heat on a flat track from previous labs. The challenge of this lab was to find a way to approximate the friction on the loop, since the normal force was very non-constant on it.

Depending on the capabilities of the students involved, there are several approximations possible.

  1. Ignore friction on the loop. It's not a large amount, and there's some leeway in the launcher settings.
  2. Assume friction on the loop is the same as it is on the flat section of the track. This is actually a fairly good approximation, but harder to justify.
  3. Approximate the normal force in the loop as a constant, that constant being the average of the normal force at the top of the loop (zero) and the bottom (weight plus centripetal acceleration). Students familiar with integration can be shown how the area under a not-quite-straight line of postive slope can be approximated by the area under a flat line at the average point between the ends of the sloped line. To find the normal force at the bottom, students will have to make further approximations to determine the speed at the bottom of the loop.
The honors students in the Gateway program proved themselves capable of working through the third approximation in the Spring 1997 quarter, but the general population of calculus-based mechanics courses may be more comfortable with one of the first two schemes.

Results

Once the students made their prediction and could back it up, the car was launched from the setting they said was the lowest possible. And in every case, the car did indeed make it through the loop without losing contact. Then, as a check, the launcher was put at one setting lower, and the car lose contact with the loop on the way through (note: this is why a car with extra mass was used. Normal cars will make it through the loop on even the lowest setting, not allowing for this kind of check). The students were generally quite pleased with the clear vindication of their work that this lab provided.

This lab, and indeed the entire course, will be used in the Autumn 1997 quarter at Ohio State for half of a class of calculus-based mechanics, the other half of the class using Dr. Van Heuvelen's current lab course. The TA training manual will be made available on the web within the next few months (I may wait until the quarter is over, to avoid some web-savvy students from looking up all the answers online).

Transparencies

Here are GIF files of the transparencies I used in the talk.

  1. Title Page
  2. Background Page 1
  3. Background Page 2
  4. Lab Page 1
  5. Lab Page 2
  6. Approximations Page 1
  7. Approximations Page 2: Not actually used in the talk, I readied this transparency in the event anyone in the audience had questions about the approximations.
Back to Education Index.