This file will remain in place for reference, but you probably want to
check out the more recent version.
"Getting Around The Coriolis Force"
David J. Van Domelen
The Ohio State University
Department of Physics
Physics Education Research Group
| Abstract
The Coriolis "force": most people know about it, but few
understand it. A simple explanation not requiring an intuitive
understanding of angular momentum is provided. Scales over which the
Coriolis Effect is relevant are also discussed.
|
1.0 Introduction and Motivation
At some point in their lives, most people hear about
the Coriolis force, whether in reference to weather patterns, sea
currents or, most prosaically, which way water flows down the sink.
Unfortunately, while many have heard of it, few understand it well enough
to explain it without resorting to vector equations.
Of course, most physics textbooks which deal with
angular kinematics will have the following equation relating the Coriolis
force to an object's mass (m), its velocity in a rotating frame
(vr) and the angular velocity of the rotating frame of
reference (w):
FCoriolis = -2 m (w x
vr)
The text will then either explain the Coriolis force in
terms of angular quantities such as conservation of angular momentum, or
will use the Coriolis force to illustrate the angular kinematics.
Unfortunately, most of us are not comfortable with angular mechanics. It
would not be an exaggeration to say that some students dread it. Nor can
we expect students to enter the classroom understanding the Coriolis
force. Hence, whether using physics to explain the phenomenon or using
the phenomenon to explain the physics, students are shaky on both sides
of this relationship.
So, what to do? This article intends to develop a
means of explaining the Coriolis effect to people who haven't yet grasped
angular mechanics. The explanation relies on linear quantities and uses
rotational concepts infrequently.
2.0. The Basic Premises
The following principles are needed before starting the
body of the explanation:
- Newton's First Law in component form - Objects in motion stay
in motion unless acted on by an unbalanced force. A vector component of
velocity will not be changed by a force perpendicular to that component.
- Spherical Geometry of the Earth - X degrees of longitude gives you
different distances between longitude lines (in miles or kilometers) at
different latitudes, plus a few additional results of being on a sphere
which will be detailed later.
- Gravity - Objects under the influence of Earth's gravity will fall
towards (and thus orbit) the center of mass of the Earth.
- Force - In one way of looking at it, a force is anything that causes a
mass to accelerate in one's frame of reference. However, most people think
of force as "something doing something to something". The Coriolis effect is
a force in the first sense, but not in the second sense: nothing is actually
pushing or pulling on anything, the acceleration is due to the fact that the
observer is moving in a circle. From this point on, the Coriolis effect will
not be directly called a force, even though that's how it's normally
characterized.
Premise 2 is probably the easiest for students to
accept, since you can draw on a globe to demonstrate that an inch is 15
degrees of longitude at one latitude and 30 degrees at another. Having a
ball or globe on hand for the explanation is generally helpful. Premises
1 and 3 require some science background, however, but should be
acceptable to students in mechanics courses.
3.0. Explanation of the Coriolis Effect
While all Coriolis-based deflection can be explained
using rotational concepts, a linear explanation is simpler if you
separate the effects into those in the north/south direction and those in
the east/west direction. The deflection of objects moving north and
south can be explained without invoking centripetal acceleration, as we
see next.
3.1. I Feel The Earth Move Under My Feet: North/South Motion
Note first that all points on the Earth have the same
rotational velocity, w (they go around once per
day). Also, places at different latitudes have different linear speeds.
A point near the equator may go around a thousand miles in an hour, while
one near the North Pole could be moving only a few dozen miles in an
hour.
Normally, objects in contact with the ground travel the
same speed as the ground they stand on. As a result, the Coriolis effect
generally doesn't have a noticeable effect to people on the ground; the
speed of the point you're standing on and the speed of the point you're
stepping onto are too close for you to tell the difference. Or, looking
back at the Coriolis effect equation above, if the velocity relative to
the rotating frame (the Earth) is zero, so is the Coriolis effect.
However, when an object moves north or south and is not
firmly connected to the ground (air, artillery fire, etc), then it
maintains its initial eastward speed as it moves. This is just an
application of Newton's First Law. An object moving east continues going
east at that speed (both direction and magnitude remain the same) until
something exerts a force on it to change its velocity. Objects launched
to the north from the equator retain the eastward component of velocity
of other objects sitting at the equator. But if they travel far enough
away from the equator, they will no longer be going east at the same
speed as the ground beneath them.
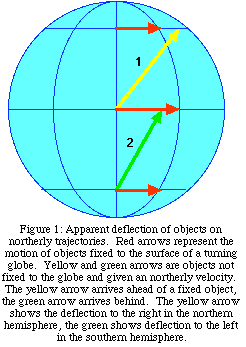 The result is that an object traveling away from the
equator will eventually be heading east faster than the ground below it
and will seem to be moved east by some mysterious "force". Objects
traveling towards the equator will eventually be going more slowly than
the ground beneath them and will seem to be forced west. In reality
there is no actual force involved; the ground is simply moving at a
different speed than its original "home ground" speed, which the object
retains.
The result is that an object traveling away from the
equator will eventually be heading east faster than the ground below it
and will seem to be moved east by some mysterious "force". Objects
traveling towards the equator will eventually be going more slowly than
the ground beneath them and will seem to be forced west. In reality
there is no actual force involved; the ground is simply moving at a
different speed than its original "home ground" speed, which the object
retains.
Consider Figure 1. Yellow arrow 1 represents an object
sent north from the equator. By the time it reaches the labeled northern
latitude, it has traveled farther east than a similar point on the ground
at that latitude has, since it kept the eastward speed it had when it
left the equator. Similarly, green arrow 2 started south of the equator
at a slower eastward speed, and doesn't go as far east as the ground at
the equator...seeming to deflect west from the point of view of the
ground.
3.2. Well, It Used To Be East: East/West Motion
In explaining how the Coriolis effect acts on objects
moving to the east or west, it helps to turn off gravity for a moment.
Don't worry, we'll turn it back on later, just be sure to put the lid
back on your coffee.
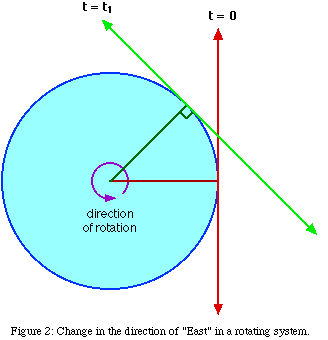 Consider being on a rotating sphere with no gravity.
An observer who is glued to the sphere throws a ball straight to the
"east" on the globe, in the direction of rotation. Since there are no
forces on the ball, it will travel in a straight line, the tangent line
shown in Figure 2 at t=0.
Consider being on a rotating sphere with no gravity.
An observer who is glued to the sphere throws a ball straight to the
"east" on the globe, in the direction of rotation. Since there are no
forces on the ball, it will travel in a straight line, the tangent line
shown in Figure 2 at t=0.
Time passes, and the ball continues on its straight
line. But the observer is attached to the globe and moves around to a
new position. At this new position, the observer's definition of the
"east" direction has changed, and is no longer the same as it was at time
t=0. The ball is no longer traveling on the observer's "east" line, and,
in fact, seems to have drifted off to one side. If the globe is spinning
slowly enough that the observer can't feel the spin, then the natural
conclusion would be that some mysterious force pushed the ball off
course, sending it drifting away from the axis of rotation more quickly
than it would go if it were still heading the "correct" easterly
direction.
Similarly, if the observer throws a ball to the west at
time t=0, it will seem to have been forced inward towards the axis of
rotation because the "west" line has moved.
Now to turn gravity back on. Gravity pulls objects
towards the center of mass of the Earth, which means it cannot change an
object's velocity in the directions perpendicular to up and down. In
other words, it won't change the east/west or north/south components of
an object's velocity.
 Figure 3 shows a slice through the Earth so that east
points out of the page. The thick arrows show the directions that
eastbound and westbound projectiles would seem to go as a result of the
Coriolis effect in the absence of gravity. The eastbound projectile (red,
upper horizontal arrow)
would seem to drift away from the axis, while the westbound projectile
(green, lower horizontal arrow)
would seem to drift towards the axis. Both of these lines
have been split into components, with one component being "up/down" and
the other being "north/south." Gravity will act against any "up"
components, and the presence of the ground will act against any "down"
components, so projectiles will stay within the light blue
"atmosphere."
Figure 3 shows a slice through the Earth so that east
points out of the page. The thick arrows show the directions that
eastbound and westbound projectiles would seem to go as a result of the
Coriolis effect in the absence of gravity. The eastbound projectile (red,
upper horizontal arrow)
would seem to drift away from the axis, while the westbound projectile
(green, lower horizontal arrow)
would seem to drift towards the axis. Both of these lines
have been split into components, with one component being "up/down" and
the other being "north/south." Gravity will act against any "up"
components, and the presence of the ground will act against any "down"
components, so projectiles will stay within the light blue
"atmosphere."
As a result of gravity pulling down on objects and the
ground holding them up, the remaining effect of the Coriolis effect on
objects heading east or west is to deflect them to the north or south.
In the northern hemisphere, objects heading east are deflected to the
south, for example. The Coriolis effect "pushes" them away from the axis,
and gravity pulls the object back down to the ground so that the
remaining effect is an apparent "push" to the south.
It's worth noting that this effect is weakest at the
equator, since there's no north/south components to "great circle" motion
moving east or west along the equator. And, of course, it's also weakest at
the poles, since there's no meaningful east or west motion. It turns out
that this effect is strongest at mid-latitudes.
4.0. Putting It Together: Low Pressure Systems
Now we've explained how things moving towards the poles
curve to the east, things moving away from the poles curve to the west,
things moving east curve towards the equator and things moving west curve
towards the poles. In other words, air (or anything else) moving freely
in the northern hemisphere deflect to the right, air moving freely in the
southern hemisphere deflect to the left. And this is what the result of
the vector cross products in the Coriolis effect equation says as well, in
its mathematical shorthand.
What does this mean for, say, weather systems? Take,
for example, a low pressure center, where there's less air than in the
area around it. If there's less air in one place than in the
surroundings, air will try to move in to balance things out.
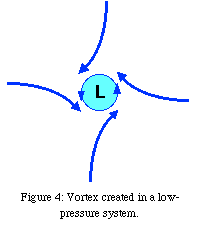 Air starting at rest with respect to the ground will
move towards a low pressure center. Such motion in the Northern
Hemisphere will deflect to its right, as shown in Figure 4. However, the
forces which got the air moving towards the low pressure center in the
first place are still around, and the result will be a vortex of air
spinning counter-clockwise. Air will try to turn to the right, the low
pressure system will try to draw the air into itself, and the result is
that air is held into a circle that actually turns to the left. Without
the Coriolis effect, fluid rushing in towards a point could still form a
vortex, but the direction would either be random or depend solely on the
initial conditions of the fluid.
Air starting at rest with respect to the ground will
move towards a low pressure center. Such motion in the Northern
Hemisphere will deflect to its right, as shown in Figure 4. However, the
forces which got the air moving towards the low pressure center in the
first place are still around, and the result will be a vortex of air
spinning counter-clockwise. Air will try to turn to the right, the low
pressure system will try to draw the air into itself, and the result is
that air is held into a circle that actually turns to the left. Without
the Coriolis effect, fluid rushing in towards a point could still form a
vortex, but the direction would either be random or depend solely on the
initial conditions of the fluid.
The eye of a hurricane is a clear example of fast winds
bent into a tight circle, moving so fast that they can't be "pulled in" to
the center. The very low pressure at the center of the hurricane means that
there is a strong force pulling air towards the center, but the high speed of
the wind invokes the Coriolis effect strongly enough that the forces reach a
kind of balance. The net force on air at the eye wall is a centripetal force
large enough to keep the air out at a given radius determined by its
speed.
5.0. Other Results and Non-Results
"Fine," you may say, "that explains storms. But what
about water going down the sink?" In fact, this question is a good
"hook" for getting students interested in the Coriolis effect in the first
place.
Because the Earth's angular velocity is so small (360
degrees per day, or about 7 x 10-5 radians per second), the
Coriolis effect isn't really significant over small distances (As equation
1 shows, high velocity also can make a difference, but for the purposes
of this paper small distance-high speed effects will not be considered).
So, what things are likely to be affected by the Coriolis effect in a
large way?
5.1. Up In The Air
Just looking at a weather system on the nightly news
gives one example that has already been addressed. Large weather systems
feature masses of air and moisture that travel hundreds of miles and can
have wind speeds reaching over a hundred miles an hour in the worst
storms.
Another example of a quickly moving object in the sky
which covers hundreds of miles is an airplane. All pilots need to have
familiarity with the effects of the Coriolis effect, since airplanes can
reach speeds much higher than even the fastest hurricane winds. Over the
course of a several hour trip, an airplane could be deflected by a
significant amount if the pilot didn't compensate for the Coriolis
effect.
Long-distance artillery may or may not be another example
of something requiring a Coriolis correction. I've seen some papers that say
it's negligible compared to the Magnus force (a result of the fact artillery
shells spin), and others that claim it is important on its own.
So, fast things moving over great distances can be
significantly affected by the Coriolis effect. But what about the
sink?
5.2. Water Going The Wrong Way Down The Sink
In a kitchen sink, of course, speeds and time scales
are much smaller than hours and miles. Water rushing down a drain flows
at speeds on the order of a meter per second in most sinks, which are
themselves less than a meter wide. Qualitatively, there doesn't seem to
be much chance for deflection. Quantitatively, putting these numbers
into Equation 1 results in an estimated change in rotation of only a
fraction of a degree per second, and a very small fraction at that...less
than an arc-second (1/3600th of a degree) per second over the course of
the entire draining of the sink, ignoring additional effects caused by
conservation of angular momentum and the like. Under extremely
controlled conditions, this can cause water to flow out of a container
counter-clockwise in the northern hemisphere and clockwise in the
southern hemisphere, but your kitchen sink is not so controlled. Things
like leftover spin from filling the sink (even when the water looks
still, it's rotating slowly for a long time after it seems to stop),
irregularities in the construction of the basin, convection currents if
the water is warmer or colder than the basin, and so forth, can affect
the direction water goes down the sink. Any one of these factors is
usually more than enough to overwhelm the small contribution of the
Coriolis effect in your kitchen sink or bathtub. Research in the 1960s
showed that if you do carefully eliminate these factors, the Coriolis
effect can be observed1,2.
Water in the sink doesn't go far enough to trigger a
noticeable north/south deflection. Most often, it simply spirals down
the sink the way it went into the sink, and the same is true of things
like the famous "demonstration" of the Coriolis effect shown at tourist
traps along the Equator (especially since east/west deflection is absent!).
Maybe there's a conspiracy to manufacture
right-handed sinks in the Northern Hemisphere and left-handed sinks in
the Southern Hemisphere? In any case, don't blame it on the Coriolis
effect unless your sink is the size of a small ocean.
Acknowledgements
Thanks to the readers of the Usenet newsgroups
alt.fan.cecil-adams and misc.education.science for asking the questions
which inspired the author to devise an explanation for the Coriolis
effect. Thanks also to Donald Shabkie, who pointed out the importance of
the Coriolis effect to aviators after seeing the above explanation online,
and to Steven Carson, who pointed out the references in Nature. Finally,
work on this paper was supported in part by NSF grants NSF GER-9553460
and NSF DUE-9396205.
Notes:
- Shapiro, 1962, Bath Tub Vortex, Nature, v 196, pp 1080-81 (Northern
Hemisphere)
- Trefethen, et.al., 1965, The Bath Tub Vortex in the Southern
Hemisphere, Nature, v 207, pp 1084-85
Back to the main Education page.